【C++】【Eigen】Eigenで高速フーリエ変換(FFT)を行う
はじめに
Eigenには、unsupportedながら高速フーリエ変換を行うライブラリが用意されています。今回、これを使用して高速フーリエ変換を行うプログラムを作成してみます。
Eigen::FFTクラス
高速フーリエ変換を行うには、Eigen::FFT<>クラスのオブジェクトを作成する必要があります。公式のEigen-unsupportedには、残念ながらこのクラスに関するドキュメントがほとんどなく、使い方がよくわかりません。しかしながら、ソースコードを見る限り使い方はほぼ決まっているようで、高速フーリエ変換を行うにはEigen::FFT<>::fwd()メソッドを、逆変換を行うにはEigen::FFT<>::inv()メソッドを呼び出すだけで良いと思われます。
#define _USE_MATH_DEFINES
#include <cmath>
#include <iostream>
#include <Eigen/Eigen>
#include <unsupported/Eigen/FFT>
int main()
{
double dt = 0.01; // サンプリング周期
size_t n = 256; // サンプル数
double f0 = 5, f1 = 10; // 周波数
Eigen::VectorXd t(n), y(n), y_ifft(n), amp(n);
Eigen::VectorXcd y_fft(n);
// 今回の例では振幅2で周波数5と振幅1で周波数10の2つの波の合成とする
for(int i = 0; i < n; i++){
t(i) = dt * i;
y(i) = 2 * std::sin(2 * M_PI * f0 * t(i)) + std::sin(2 * M_PI * f1 * t(i));
}
Eigen::FFT<double> fft;
fft.fwd(y_fft, y); // フーリエ変換を実施
amp = (y_fft / (n / 2)).cwiseAbs(); // 振幅の計算
fft.inv(y_ifft, y_fft); // 逆フーリエ変換を実施
for(int i = 0; i < n; i++){
std::cout << (dt * i) << '\t' << y(i) << '\t' << y_ifft(i) << '\t' << (i / dt / n) << '\t' << amp(i) << std::endl;
}
return 0;
}Eigen::FFT<>::fwd()メソッドで変換される結果は複素数なので、メソッドの第1引数として渡す変数はVectorXcd型で宣言しています。
なお、Eigen::FFT<>::fwd()、Eigen::FFT<>::inv()ともに、Eigenのベクトルオブジェクトだけでなく、std::vector<>も引数として渡すことができるように定義されています。その場合は、以下のようになります。
#include <vector>
#include <complex>
// (略)
std::vector<double> y, y_ifft;
std::vector< std::complex<double> > y_fft;
//(略)
Eigen::FFT<double> fft;
// 使い方はVectorXd版と同じ
fft.fwd(y_fft, y);
fft.inv(y_ifft, y_fft);先のコードの出力結果をExcelで出力してみました。
まずは元の信号です。
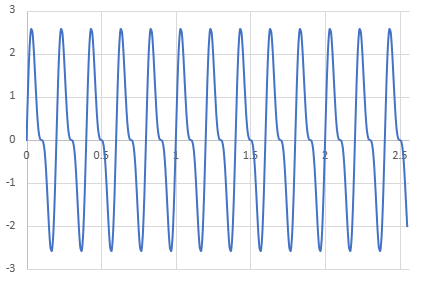
続いて振幅です。0~50の範囲で表示しています。見てわかるように、周波数5と10のところに、ピークが立っています。
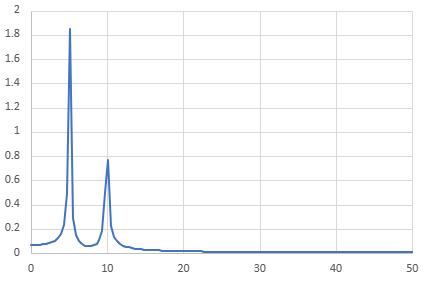
最後に復元した信号です。元の信号と同じ形をしていることがわかります。
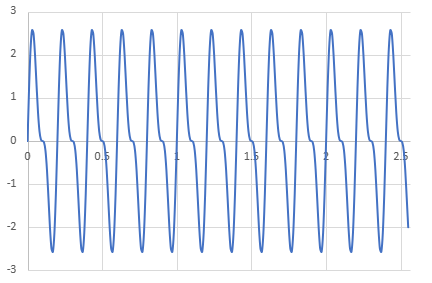
まとめ
Eigenで高速フーリエ変換を使う方法をまとめます。
Eigen::FFT<>クラスのオブジェクトを作成する。- フーリエ変換を行うには
Eigen::FFT<>::fwd()メソッドを使用する。 - 逆変換を行うには
Eigen::FFT<>::inv()メソッドを使用する。



ディスカッション
コメント一覧
まだ、コメントがありません