【Python】単純移動平均を利用したバックグラウンド推定

2024-06-14python,スペクトル,バックグラウンド,ベースライン,信号処理,化学

スペクトル等のデータから定量計算を行うためには、あらかじめバックグラウンドを除去しておくことが有効です。直線近似など簡単な方法でバックグラウンドを見積もれることもありますが、複雑なバックグラウンド形状の場合はそれが容易ではない場合も多くあります。

そのような場合に、有効な手法として単純移動平均を繰り返すことでスペクトル等のデータを処理し、バックグラウンドを見積もる方法があります。このエントリでは、その手法について説明します。

単純移動平均の性質

単純移動平均とは、ある任意の点$(x_{i}, y_{i})$と隣り合う$N$個の点$(x_{i-N}, y_{i-N}), \dots, (x_{i}, y_{i}), \dots, (x_{i+N}, y_{i+N})$について、平均値

$$
\displaystyle
\bar{y}_{i} = \frac{1}{2N+1}\sum^{N}_{j=-N}y_{i+j}
$$

をとり、$y_{i}$を$\bar{y}_{i}$に置き換えていくことを繰り返す手法です。ノイズを含むデータをスムージングするのに使われることがあります。このとき、$N$を大きくするとノイズが強く抑えられますが、その分副作用も強く働きます。

以下にピークを含むデータに対して単純移動平均を実施した例を示します。

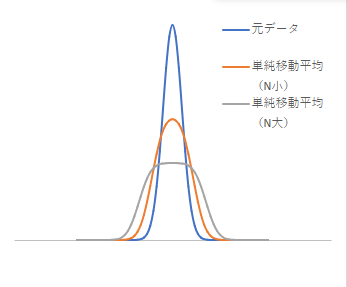
moving_avrage.png

平均を取る各点が等しい重みを持つため、ピークに近いバックグラウンドではピーク部分の影響を強く受け、逆にピーク部分ではバックグラウンドの影響を強く受けることになります。その結果、ピークは小さくなり、裾野が広がった形へ変形します。

バックグラウンドの推定

単純移動平均を利用したバックグラウンドの推定では、この性質を利用します。あえて大きな$N$で単純移動平均を取ることで、ピークを均します。そして、元のデータと比較し、値の小さい方を採用することで新しいデータ(1)とします。

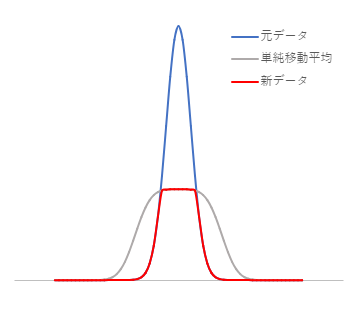
newdata1.png

新しいデータ(1)に対して、再び単純移動平均を取り、新しいデータ(1)と比較して値の小さいほうを採用し、新しいデータ(2)とします。これを繰り返すとやがてバックグラウンドと同レベルまでピークが均されます。

以下にこの操作を10回繰り返した例を示します。バックグラウンド近くまでピークが均されていることがわかります。あと何回か繰り返せば、バックグラウンドとみなしてもよさそうです。

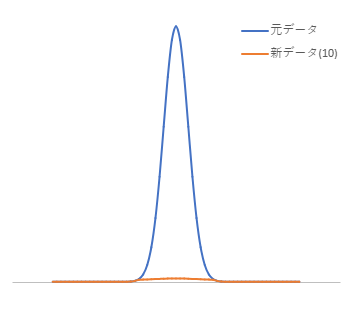
newdata10.png

バックグラウンドが平らでなくとも、比較的平坦なところではこの手法が有効に使えます。以下は、緩やかな曲線のバックグラウンドを持つピークに対して適用した事例です。こちらも操作を10回繰り返しています。

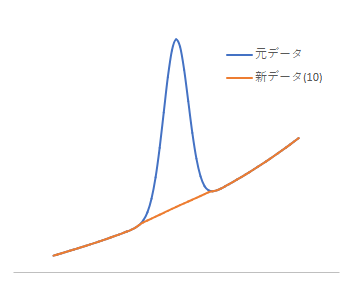
newdata10-2.png

この手法は処理が比較的高速に行えるので便利です。一方、何回操作を繰り返すか、$N$をいくつにするかなどユーザーに判断を委ねられるところがあります。データによるので判断は難しいですが、たとえば参考文献[1]では、$N$をピークのFWHMの2～4倍に設定するのがtypicalであると述べています。

ノイズを含むデータへの適用

上の説明では滑らかなデータを用いましたが、実際のデータではノイズ成分を含んでいることがほとんどです。元データがノイズを含む場合に、上記手法を適用した場合、どのようになるか実験してみました。

元データは、適当な関数を合成して作成した複数のピークを含む滑らかなデータに対して、ホワイトノイズを付加した疑似スペクトルで、データ点数は1000点です。このデータについて、$N=20$で単純移動平均を取る操作を20回ないし100回繰り返しました。なお、両端$N$点は処理せず、オリジナルのデータを残しました。

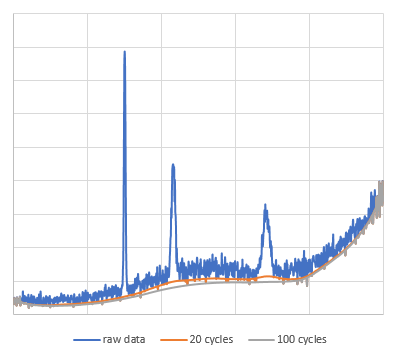
noisydata.png

この結果を見る限り、20回も繰り返せば十分バックグラウンドの推定ができそうに思えます。また、あまり繰り返すと山なりのバックグラウンドも均されていまい、バックグラウンドを低く見積りすぎてしまう様子も観察できました。回数は多ければ多いほど良いというわけではなさそうです。

なお、移動平均と元データの低い方の値を採用するという方法のため、ノイズを含むデータの場合にはノイズの低いレベルにバックグラウンドが合わせられます。そのため、Savitzky-Golay法やWhittaker Smoother等であらかじめスペクトルのスムージング処理をかけておくと、より良いバックグラウンドが推定できる可能性があります。

参考文献

  1. Brückner, S. Estimation of the Background in Powder Diffraction Patterns through a Robust Smoothing Procedure J. Appl. Cryst.2000, 33, 977-979.

Pythonでの実装

以上の動作をPythonで実装してみました。以下のように非常に短いコードで書くことができます。

単純移動平均はNumpyのconvolve()を使うと簡単に実施できます。また要素ごとの比較もNumpyなら1行で行うことが可能です。

import numpy as np

def estimate_background_with_moving_average(y, points, cycles):
    n = 2 * points + 1
    y_tmp = y.copy()

    for i in range(cycles):
        y_old = y_tmp.copy()
        y_tmp[points:-points] = np.convolve(y_old, np.ones(n) / n, mode='valid')
        y_tmp = np.where(y_tmp > y_old, y_old, y_tmp)

    return y_tmp

まとめ

単純移動平均を利用してバックグラウンドを推定する方法について紹介しました。動作の概要をまとめると以下のようになります。

  1. 任意の点数$N$で単純移動平均をとり、元のデータと比較する。
  2. 小さい値を採用し、新しいデータとする。
  3. 新しいデータに対して、1を再度適用する。
  4. 適当な回数繰り返す。

また、上に示したようにPythonでは比較的簡単なコードで実現できます。Numpyのような強力なライブラリがない他の言語でもそれほど複雑なコードにはならないと思われます。

python,スペクトル,ベースライン,信号処理

Posted by izadori