【C++】【Eigen】Asymmetric Least Squares Smoothing（AsLS法）によるバックグラウンド推定

2024-01-232024-04-16C++,Eigen,スペクトル,信号処理

前回のエントリでは、単純移動平均を利用したバックグラウンドの推定法を紹介しました。本記事では、Whittaker Smootherを利用したバックグラウンド推定法である、Asymmetric Least Squares Smoothing（AsLS法、ALS法とも略されることがある）について紹介したいと思います。

1. Whittaker Smootherの性質
2. AsLS法の原理
- 2.1. 参考文献
3. Eigenによる実装例
- 3.1. 動作を確認した環境
- 3.2. ノイズを含むデータへの適用
4. まとめ

Whittaker Smootherの性質

Whittaker Smootherについては、以下のエントリをご覧ください。

【C++】【Eigen】Whittaker Smootherを実装する

スペクトル等のノイズを含むデータをスムージングするために広く使われる手法の1つにSavitzky-Golay法 ...

https://izadori.net/math-whittaker/

簡単におさらいすると次のようになります。観測された測定データの列を$\boldsymbol{y}$に対して、滑らかなデータ列$\boldsymbol{z}$を適合させることを考えると、$\boldsymbol{y}$に対する$\boldsymbol{z}$の適合度合いと$\boldsymbol{z}$の粗さという2つの要素からなる、ペナルティ付き最小二乗法問題に帰着します。

$$
\displaystyle
Q = \sum_{i}w_{i}(y_{i} – z_{i})^{2} + \lambda\sum_{i}(\Delta^{s}z_{i})^{2}
\tag{1}
$$

ここで$w_{i}$は重み、$\lambda$はペナルティ係数、$s$は差分の回数です。重み$w_{i}$については後ほど考慮するとして、ここではペナルティ係数$\lambda$について考えます。スムージングを目的とする場合、$\lambda$は1などとして、通常あまり大きな値は使いません。しかし、ここではあえて極端に大きな値を設定した場合の挙動を見てみます。

式(1)の第二項は粗さに関する項目です。$\lambda$を大きくすると粗さに関する項目が優勢となり、より滑らかな線が得られることが予想されます。単純なガウシアンピークに対して、$\lambda$を大きくしたWhittaker Smoother($s = 2$)を適用した結果を以下に示します。

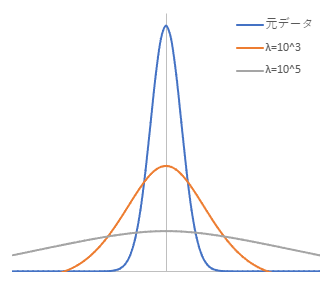
図からわかるように、$\lambda$を大きくすることによって元の曲線から外れてピークが低くなり、裾野が広がった形へと変形します。単純移動平均の性質と似たような傾向が見られます。AsLS法でもこの性質を利用します。

AsLS法の原理

単純移動平均を利用したバックグラウンドの推定では、元のデータと単純移動平均を取ったデータを比較し、値の小さい方を採用するという方法を取っていましたが、AsLS法では重み$w_{i}$を活用します。

具体的には重みパラメータ$p$を用い、$y_{i} > z_{i}$となる点に対しては重み$w_{i} = p$を与え、逆に$y_{i} <= z_{i}$となる点に対しては重み$w_{i} = 1 - p$を与えます。そして再びWhittaker Smootherを実施します。これを重み$w_{i}$が変わらなくなるまで繰り返します。

考え方は、$y_{i} > z_{i}$となる点はピークが均された部分とみなして小さな重み$p$を与えることで、スムージングに対する重要度を下げ、よりベースラインに近い部分の点の重要度を高く保つことです。これにより、ベースラインに近い部分の点に適合した滑らかな曲線が生成されることとなります（この部分がasymmetricと付いている所以です）。

$p$は小さい値である必要があるため、0.5より小さな値を設定しますが、Eilersによると$0.001 \leqq p \leqq 0.1$がgood choiceであると述べています。また、$\lambda$は$10^{2} \leqq \lambda \leqq 10^{9}$がよい（もちろん例外もある）とも述べています[1]。

参考文献

Eilers, P. H. C.; Boelens, H. F. M. Baseline Correction with Asymmetric Least Squares Smoothing Leiden University Medical Centre Report2005, 1(1), 1-5.

Eigenによる実装例

参考文献[1]には、MATLABのコードが載っており、自分で実装するのは比較的簡単です。これを元に、C++とEigenで実装しました。もっとも、このコードは繰り返し回数が10回に固定されており、より汎用的にするには多少修正が必要です（Eilersは5～10回もあれば十分だと言っていますが）。念のため繰返し回数も設定できるようにしました。

コードをGitHubにも公開しましたので、興味のある方はご覧ください。なお、ビルドにはwhittaker.h, whittaker.cpp, diff.hが必要です。これらのコードもGitHub上に置いてあります。あわせてダウンロードしてください。

asls.h

#ifndef __IZADORI_EIGEN_ASLS_H__
#define __IZADORI_EIGEN_ASLS_H__

#include "whittaker.h"

// AsLS法によるバックグラウンド推定
//
// y       : 実際の観測データ
// lambda  : 平滑化のためのペナルティ係数
// p       : 重み
// maxloop : 最大繰返し回数
// loop    : 実際の繰返し回数（戻り値）
const Eigen::VectorXd BackgroundEstimation_AsLS(
  const Eigen::VectorXd & y, const double lambda, const double p,
  const unsigned int maxloop, unsigned int & loop
);

#endif // __IZADORI_EIGEN_ASLS_H__

asls.cpp

#include "asls.h"

const Eigen::VectorXd BackgroundEstimation_AsLS(
  const Eigen::VectorXd & y, const double lambda, const double p,
  const unsigned int maxloop, unsigned int & loop
)
{
  size_t m = y.size();

  loop = 0;
  Eigen::VectorXd w, w0, z, pv(m), npv;

  w.setOnes(m);
  w0.setZero(m);
  pv.fill(p); npv = (1 - pv.array()).matrix();

  while(loop < maxloop)
  {
      z = WhittakerSmoother(y, w, lambda, 2);

      // 重みwの更新
      w = (y.array() > z.array()).select(pv, npv);

      // 収束判定
      if(((w.array() - w0.array()).abs() < 1e-6).all())
      {
          break;
      }

      w0 = w;
      loop++;
  }

  return z;
}

動作を確認した環境

OS
1. Windows 10
  1. Microsoft C/C++ Optimizing Compiler 19.28.29913 for x64
  2. MinGW-W64 GCC version 8.1.0
  3. Clang version 11.0.1
2. Linux
  1. GCC version 9.3.0
Eigen version 3.3.9

ノイズを含むデータへの適用

上記コードを用いて、ノイズを含むデータに適用し、どのようなバックグラウンドが生成されるか実験してみました。

元データは、適当な関数を合成して作成した複数のピークを含む滑らかなデータに対してホワイトノイズを付加した疑似スペクトルで、データ点数は1000点です。このデータについて、$\lambda$を$10^{3}, 10^{6}, 10^{9}$とした場合を評価してみました。$p$は0.01、最大繰返し回数は100回としています。

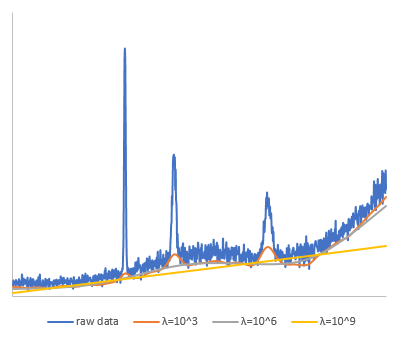
この結果を見ると、$\lambda = 10^{3}$ではピーク部分のバックグラウンドを大きく見積もりすぎており、$\lambda = 10^{9}$ではバックグラウンドが大きく外れる結果となりました。$\lambda$はあまり大きすぎても良くないようです。今回は、$\lambda = 10^{6}$が良い感じにバックグラウンドを見積もれています。

なお、収束回数はそれぞれ5回、6回、6回でした。