【C++】【Eigen】Levenberg-Marquardt法を実装する
観測データをあるモデルで回帰する場合に、最小二乗法がよく使われます。以前のエントリでは、最小二乗法の解法の一つであるGauss-Newton法について調べました。今回は、Levenberg-Marquardt法について調べて見たので、以下にまとめました。また、C++での実装例も紹介します。
https://izadori.net/math-gauss-newton/Gauss-Newton法と最急降下法
Gauss-Newton法は
$$
S(\boldsymbol{x}, \boldsymbol{a}) = \frac{1}{2}\sum^{n}_{i=1}(f(\boldsymbol{x}_{i}, \boldsymbol{a}) – y_{i})^{2} \tag{1}
$$
の2階微分
$$
\displaystyle
\begin{split}
\frac{\partial^{2} S}{\partial a_{k}\partial a_{j}}
&= \frac{\partial}{\partial a_{k}}\Bigl\{\sum^{n}_{i=1}\Bigl(\frac{\partial f(\boldsymbol{x}_{i}, \boldsymbol{a})}{\partial a_{j}}(f(\boldsymbol{x}_{i}, \boldsymbol{a}) – y_{i})\Bigr)\Bigr\} \\
&= \sum^{n}_{i=1}\Bigl(\frac{\partial^{2}f(\boldsymbol{x}_{i}, \boldsymbol{a})}{\partial a_{k} \partial a_{j}}(f(\boldsymbol{x}_{i}, \boldsymbol{a}) – y_{i}) + \frac{\partial f(\boldsymbol{x}_{i}, \boldsymbol{a})}{\partial a_{j}}\frac{\partial f(\boldsymbol{x}_{i}, \boldsymbol{a})}{\partial a_{k}}\Bigr)
\end{split} \tag{2}
$$
からHessian部分を省略した
$$
\displaystyle
\boldsymbol{H} \approx \boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f} \tag{3}
$$
$$
\displaystyle
\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f} \Delta \boldsymbol{a}= -\boldsymbol{J}_{f}^{T} \boldsymbol{r} \tag{4}
$$
を使ってパラメータを更新する方法でした（$\boldsymbol{J}_{f}$は$f(\boldsymbol{x},\boldsymbol{a})$のJacobian）。この方法は収束が早いものの、$S$が必ず減少する方向にパラメータが更新されるとは限りません。
一方、Sが必ず減少する方向にパラメータを更新できる方法として、最急降下法があります。
(1)をパラメータ$\boldsymbol{a}$で偏微分したベクトルを$\nabla \boldsymbol{S}$
$$
\displaystyle
\nabla \boldsymbol{S} =
\begin{pmatrix}
\frac{\partial S}{\partial a_{0}} \\
\vdots \\
\frac{\partial S}{\partial a_{m}}
\end{pmatrix} = \boldsymbol{J}_{f}^{T} \boldsymbol{r} \tag{5}
$$
と置くと、最急降下法は次のように表されます。
$$
\displaystyle
\Delta \boldsymbol{a} = -k \nabla \boldsymbol{S} = -k \boldsymbol{J}_{f}^{T} \boldsymbol{r} \tag{6}
$$
しかしこの方法は、$S$の勾配($\nabla \boldsymbol{S}$)に大きく依存し、勾配が緩やかになるにつれて収束が遅くなるという欠点があります。
そこで、(3)を修正して最急降下法的要素を取り入れ、パラメータ更新後の$S$の値が減少するのであれば、最急降下法的要素を弱め、反対に$S$が増加するのであれば、最急降下法的要素を強める方法が考案されました。これがLevenberg-Marquardt法です。
Levenberg-Marquardt法
Levenberg-Marquardt法では、(4)の代わりに
$$
\displaystyle
(\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f} + \lambda \boldsymbol{I}) \Delta \boldsymbol{a}= -\boldsymbol{J}_{f}^{T} \boldsymbol{r} \tag{6}
$$
を使ってパラメータを更新していきます。$\lambda$は最急降下法的要素の度合いを調整するパラメータです。パラメータを更新後にSが減少した場合は$\lambda$を$1/c$倍します。反対に$S$が増加した場合は、$c$倍します。定数$c$は$2$や$10$などが使われることが多いようです。
$\lambda$が小さいときには、$\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f} + \lambda \boldsymbol{I}$の対角要素は$\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f}$に近くなり、Gauss-Newton法とほぼ同じになります。$\lambda$を大きくすることで、徐々に$\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f}$は小さくなり、最急降下法に近くなります。
Eigenでの実装
Eigenを使ったC++の実装例です。
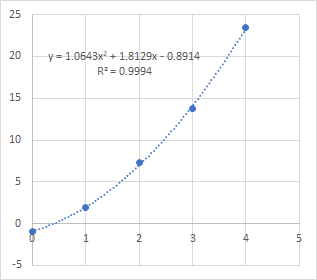
Gauss-Newton法の時と同じく、点$(x, y) = (0, -0.9), (1, 1.9), (2, 7.3), (3, 13.8), (4, 23.5)$を2次関数$f(x) = a_{0} + a_{1} x + a_{2} x^{2}$で回帰してみました。
ラムダ式で関数$f$とその偏微分$g$を与え、係数$a$の初期値を適当に与えた後に、LevenbergMarquardt()を呼び出して計算します。なお、テンプレートで作成しているので、ラムダ式である必要はなく、operator ()を実装したクラスでも動作します。
GitHubにもソースコードをアップしました。
#include <iostream>
#include <Eigen/Eigen>
//---------------------------------------------
// 関数fのJacobianを計算する
//---------------------------------------------
template <typename Grad>
Eigen::MatrixXd CalcJacobian(
Grad & g, Eigen::VectorXd & a, Eigen::VectorXd & x
)
{
Eigen::MatrixXd ret;
ret.resize(x.size(), a.size());
for (unsigned int i = 0; i < x.size(); i++){
auto grad = g(a, x(i));
for(unsigned int j = 0; j < a.size(); j++){
ret.row(i) = grad;
}
}
return ret;
}
//---------------------------------------------
// Levenberg-Marquardt法の計算
//---------------------------------------------
template <typename Func, typename Grad>
bool LevenbergMarquardt(
Func & f, Grad & g, Eigen::VectorXd & a, Eigen::VectorXd & x, Eigen::VectorXd & y,
const double eps, const unsigned int max_loop
)
{
// ループ回数
unsigned int loop = 0;
// ステップ数の初期値
double alpha = 1;
// ステップ数の係数
double c = 10;
// 残差二乗和
double s_new, s_old = 0;
while(true){
// 関数fのJacobianの計算
Eigen::MatrixXd jac = CalcJacobian(g, a, x);
// 関数fの計算
Eigen::VectorXd fx(x.size());
for(unsigned int i = 0; i < x.size(); i++){
fx(i) = f(a, x(i));
}
// 残差ベクトルrの計算
Eigen::VectorXd r = fx - y;
// 残差二乗和の計算
s_new = r.squaredNorm();
// 収束判定
if(std::fabs(s_new - s_old) < std::fabs(eps)){
break;
}
alpha *= (s_old > s_new) ? (1 / c) : c;
s_old = s_new;
//---------------------------
// パラメータaの更新
//---------------------------
// Δaの計算
Eigen::MatrixXd h = jac.transpose() * jac + alpha * Eigen::MatrixXd::Identity(jac.cols(), jac.cols());
Eigen::VectorXd delta_a = h.ldlt().solve(-jac.transpose() * r);
// パラメータaの更新
a += delta_a;
// ループ回数のチェック
if(loop >= max_loop){
break;
}
loop++;
}
return (loop < max_loop);
}
//---------------------------------------------
// main()関数
//---------------------------------------------
int main()
{
Eigen::VectorXd a(3), x(5), y(5);
a << 1, 1, 1;
x << 0, 1, 2, 3, 4;
y << -0.9, 1.9, 7.3, 13.8, 23.5;
// 関数f
auto f = [](Eigen::VectorXd & a, double x){
return a(0) + a(1) * x + a(2) * x * x;
};
// 勾配ベクトルg
auto g = [](Eigen::VectorXd & a, double x){
Eigen::VectorXd ret(3);
ret << 1, x, (x * x);
return ret;
};
if(LevenbergMarquardt(f, g, a, x, y, 1.0e-6, 100)){
std::cout << a << std::endl;
}
else{
std::cout << "failure." << std::endl;
}
return 0;
}出力結果
-0.891429
1.81286
1.06429Gauss-Newton法で計算した結果と同じ結果が得られました。
Excelで散布図を作り、2次関数で回帰した結果とも当然一致しています。
まとめ
Levenberg-Marquard法について説明とC++による実装例を紹介しました。
アルゴリズムについてまとめると以下のようになります。
Levenberg-Marquard法のアルゴリズム
- パラメータ$a$の初期値を決める
- 残差ベクトル$\boldsymbol{r}$と関数$S$を計算する
- 関数$f$のJacobianを計算する($\boldsymbol{J}_{f})$
- $(\boldsymbol{J}_{f}^{T} \boldsymbol{J}_{f} + \lambda\boldsymbol{I})\Delta \boldsymbol{a} =-\boldsymbol{J}_{f}^{T} \boldsymbol{r}$からパラメータの変化量$\Delta \boldsymbol{a}$を求める
- $\boldsymbol{a}$を更新する
- 残差ベクトル$\boldsymbol{r}$と関数$S$を計算する
- 関数$S$が前回の値より大きくなっていた場合は$\lambda$を$c$倍、そうでなければ$1/c$倍する
- 関数$S$の変化量がしきい値以下なら計算終了
- 3に戻る