【C++】【Eigen】AsLS法の改良 – airPLS法とarPLS法
以前のエントリでは、Whittaker Smootherを利用したAsymmetric Least Squares Smoothing(AsLS法)によるバックグラウンド推定の方法を紹介しました。本記事では、このAsLS法を改良した手法である、adaptive iteratively reweighted Penalized Least Squares(airPLS法)とasymmetrically reweighted Penalized Least Squares(arPLS法)について紹介したいと思います。
AsLS法のおさらい
AsLS法については、以下のエントリをご覧ください。
AsLS法は、Whittaker Smoother
$$
\displaystyle
Q = \sum_{i}w_{i}(y_{i} – z_{i})^{2} + \lambda\sum_{i}(\Delta^{s}z_{i})^{2}
\tag{1}
$$
を繰り返し適用することで、ピークを均していく手法です。ここで$w_{i}$は重み、$\lambda$はペナルティ係数、$s$は差分の回数です。粗さを表す第2項を優勢とするため、ペナルティ係数$\lambda$に意図的に大きな値を与え、ピークを潰します。
元のデータと比較し、再度Whittaker Smootherを適用します。この時重み$w_{i}$を元のデータを比較した結果に応じて変化させます。重みパラメータ$p$を用い、$y_{i} > z_{i}$となる点に対しては重み$w_{i} = p$を与え、逆に$y_{i} <= z_{i}$となる点に対しては重み$w_{i} = 1 - p$を与えます。これは、元のデータがスムージング後のデータより大きい点に対して、重要度を下げることを意味します。このようにすることで、ベースライン近傍のデータだけがしだいに残っていきます。重み$w_{i}$が変化しなくなったら、反復計算を終了させます。
AsLS法は、コードも比較的シンプルで強力な手法ですが、課題もあります。それは、パラメータ$p$をどのように設定するかということです。また、$y_{i} > z_{i}$となる点に対して一律で重み$w_{i} = p$を与えるため、実際はバックグラウンドであっても$y_{i} > z_{i}$となった点については重要度がかなり下げられてしまいます。結果として、ノイズの低いレベルにバックグラウンドが合わせられることになります。
本記事で紹介するairPLS法とarPLS法は、このような課題に対応した手法となります。
airPLS法とarPLS法
airPLS法
airPLS法は2010年にZhangらによって発表されたAsLS法の改良手法です[1]。著者による論文原稿やMATLAB、R、Pythonによる実装がGitHubにて公開されています。
airPLS法では、重み$w_{i}$を以下のように決定します。
$$
w_{i} =
\begin{cases}
0 & y_{i} \geqq z_{i} \\
e^{\frac{t|y_{i} – z_{i}|}{|\mathbf{d}|}} & y_{i} < z_{i}
\end{cases}
$$
ここで$t$は反復の回数、$\mathbf{d}$は、$y_{i} < z_{i}$となる点のみ取り出したベクトルです。 $y_{i} \geqq z_{i}$の時は、重みを0とすることで次回の計算では除外されます。一方、$y_{i} < z_{i}$では重み$w_{i}$は指数関数で計算されます。指数部分の値は0以上の値をとるので、重み$w_{i}$は1以上の値となることが予想されます。 このことから、airPLS法では、$y_{i} \geqq z_{i}$となる点の重要度はなくなり、$y_{i} < z_{i}$となる点の重要度がAsLS法以上に高くなります。
ちなみに絶対値の記号が紛らわしいですが、著者のPythonでの実装を見ると$|\mathbf{d}|$は
dssn = np.abs(d[d < 0].sum())となっています。$y_{i} < z_{i}$となる点の合計の絶対値として計算されます。ベクトルの大きさではないので注意が必要です。
また、論文では指数関数の指数部分の分子が$t(y_{i} – z_{i})$となっています。しかしながら、著者のPythonでの実装を見ると
w[d < 0] = np.exp(i * np.abs(d[d < 0]) / dssn)
w[0] = np.exp(i*(d[d < 0]).max() / dssn)
w[-1] = w[0]なんと絶対値を取っています(本記事では絶対値に直しました)。さらに両端の重みは違う計算を行っています。これは実装を見ないとわかりません。
収束判定は以下の式で行われます。
$$
|\mathbf{d}| < 0.001 \times |\mathbf{y}|
$$
この収束判定の式は大変紛らわしいです。著者のPythonでの実装を見ると、収束判定部は
dssn < 0.001 * (abs(y)).sum()となっています。$|\mathbf{d}|$が 「合計の絶対値」 を取っていたのに対し、$|\mathbf{y}|$は 「絶対値の合計」 となります。これも著者による実装がなかったら絶対にわかりません。
airPLS法は、ベースライン推定法の論文ではよくベンチマークとして使われます。$y_{i} \geqq z_{i}$となる点の重要度がなくなる一方で、$y_{i} < z_{i}$となる点の重要度がAsLS法以上に高くなることから、ノイズの低いレベルにバックグラウンドが合わせられるという課題は残ったままです。
arPLS法
arPLS法は2015年にBaekらによって発表されたAsLS法の改良手法です[2]。著者による論文原稿が公開されています。
arPLS法では重み$w_{i}$を以下のように決定します。
$$
w_{i} =
\begin{cases}
\frac{1}{1 +\exp\left({\frac{2(d_{i} – (-m_{\mathbf{d}^{-}}+2\sigma_{\mathbf{d}^{-}}))}{2\sigma_{\mathbf{d}^{-}}}}\right)} & y_{i} \geqq z_{i}\\
1 & y_{i} < z_{i}
\end{cases}
$$
ここで、$d_{i} = y_{i} – z_{i}$です。$\mathbf{d} = \mathbf{y} – \mathbf{z}$としたとき、$y_{i} < z_{i}$となる部分のみからなるベクトルを$\mathbf{d}^{-}$と定義します。$m_{\mathbf{d}^{-}}$と$\sigma_{\mathbf{d}^{-}}$はそれぞれ$\mathbf{d}^{-}$の平均値と標準偏差です。
指数関数部分が複雑ですが、この関数はロジスティック関数です。ロジスティック関数はS字型のカーブを持つ関数で、統計学で広く使われているものです。0から1の間の値を取る特性を持っています。arPLSではこの特性を重みづけに利用しています。
同じ$y_{i} \geqq z_{i}$となる領域であっても、ベースライン上のノイズのように$y_{i}$と$z_{i}$の差が小さいところでは比較的大きな重みが与えられ、ピークのように差が大きいところでは0に近い値が与えられることになります。このようにすることによって、ノイズの低いレベルにバックグラウンドが合わせられるという課題に対処しています。
収束判定は以下の式で行われます。
$$
\frac{|\mathbf{w}^{t} – \mathbf{w}^{t + 1}|}{|\mathbf{w}^{t}|} < ratio
$$
重みを更新して更新前の重みと差を取ります。その大きさと更新前の重みの大きさの比がある値より小さくなったときに計算が終了します。
参考文献
Eigenによる実装例
airPLS法は著者のGitHubにMATLABやPythonによる実装があり、またarPLS法も参考文献[2]にMATLABのコードが載っているので、自分で実装するのは比較的簡単です。これを元に、C++とEigenで実装しました。
コードをGitHubにも公開しましたので、興味のある方はご覧ください。なお、ビルドにはwhittaker.h, whittaker.cpp, diff.hが必要です。これらのコードもGitHub上に置いてあります。あわせてダウンロードしてください。
airPLS法
- airpls.h
#ifndef __IZADORI_EIGEN_AIRPLS_H__
#define __IZADORI_EIGEN_AIRPLS_H__
#include "whittaker.h"
// airPLS法によるバックグラウンド推定
//
// y : 実際の観測データ
// lambda : 平滑化のためのペナルティ係数
// diff : 差分の次数(1~3)
// maxloop : 最大繰返し回数
// loop : 実際の繰返し回数(戻り値)
const Eigen::VectorXd BackgroundEstimation_airPLS(
const Eigen::VectorXd & y, const double lambda, const unsigned int diff,
const unsigned int maxloop, unsigned int & loop
);
#endif // __IZADORI_EIGEN_AIRPLS_H__- airpls.cpp
#include "airpls.h"
const Eigen::VectorXd BackgroundEstimation_airPLS(
const Eigen::VectorXd & y, const double lambda, const unsigned int diff,
const unsigned int maxloop, unsigned int & loop
)
{
size_t m = y.size();
loop = 0;
Eigen::VectorXd w(m), z, d;
double y_abs_sum, d_sum_abs;
w.setOnes(m);
y_abs_sum = y.array().abs().matrix().sum();
while (loop < maxloop)
{
z = WhittakerSmoother(y, w, lambda, diff);
d = (y.array() >= z.array()).select(0, y - z);
d_sum_abs = std::fabs(d.sum());
// 収束判定
if (d_sum_abs < 0.001 * y_abs_sum)
{
break;
}
// 重みwの更新
loop++;
w = (y.array() >= z.array()).select(0, ((loop * d.array().abs()) / d_sum_abs).exp());
w(0) = w(w.size() - 1) = std::exp((loop * d.maxCoeff() / d_sum_abs));
}
return z;
}arPLS法
- arpls.h
#ifndef __IZADORI_EIGEN_ARPLS_H__
#define __IZADORI_EIGEN_ARPLS_H__
#include "whittaker.h"
// arPLS法によるバックグラウンド推定
//
// y : 実際の観測データ
// lambda : 平滑化のためのペナルティ係数
// ratio : 収束判定のしきい値
// maxloop : 最大繰返し回数
// loop : 実際の繰返し回数(戻り値)
const Eigen::VectorXd BackgroundEstimation_arPLS(
const Eigen::VectorXd & y, const double lambda, const double ratio,
const unsigned int maxloop, unsigned int & loop
);
#endif // __IZADORI_EIGEN_ARPLS_H__- arpls.cpp
#include <limits>
#include "arpls.h"
const Eigen::VectorXd BackgroundEstimation_arPLS(
const Eigen::VectorXd & y, const double lambda, const double ratio,
const unsigned int maxloop, unsigned int & loop
)
{
size_t m = y.size();
loop = 0;
Eigen::VectorXd w(m), wt, z, d, tmp;
double mean, sd;
Eigen::Index ct;
// オーバーフロー対策
const double overflow = std::log(std::numeric_limits<double>::max()) / 2;
w.setOnes(m);
while (loop < maxloop) {
z = WhittakerSmoother(y, w, lambda, 2);
d = y - z;
ct = (d.array() < 0).count();
mean = (d.array() < 0).select(d, 0).sum() / ct;
sd = std::sqrt((d.array() < 0).select((d.array() - mean).matrix(), 0).squaredNorm() / (ct - 1));
tmp = ((d.array() + mean - 2 * sd) / sd).matrix();
tmp = (tmp.array() >= overflow).select(0, (1.0 / (1 + (2 * tmp).array().exp())).matrix());
// 重みwの更新
wt = (d.array() >= 0).select(tmp, 1);
// 収束判定
if ((w - wt).norm() / w.norm() < ratio) {
break;
}
w = wt;
loop++;
}
return z;
}arPLS法では指数関数の中身が大きな値となりやすく、比較的簡単にオーバーフローします。そのため対策を入れてあります。doubleの最大値の対数を取って指数関数がオーバーフローしない最大値を調べておき、指数関数の中身がこの値を超える場合は、ロジスティック関数の結果を0としてしまいます。
動作を確認した環境
- OS
- Windows 10
- Microsoft C/C++ Optimizing Compiler 19.44.35207.1 for x64
- MinGW-W64 GCC version 13.2.0
- Clang version 20.1.0
- Linux
- GCC version 12.2.0
- Windows 10
- Eigen version 3.4.0
ノイズを含むデータへの適用
上記コードを用いて、ノイズを含むデータに適用し、どのようなバックグラウンドが生成されるか実験してみました。
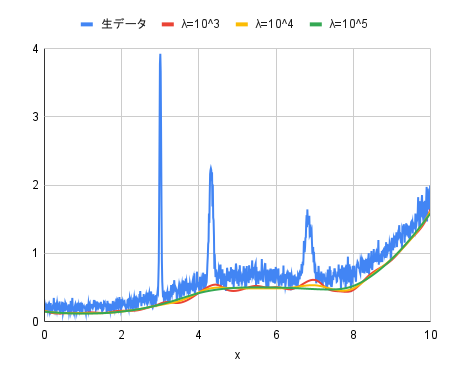
元データは、適当な関数を合成して作成した複数のピークを含む滑らかなデータに対してホワイトノイズを付加した疑似スペクトルで、データ点数は1000点です。
このデータに対して、airPLS法、arPLS法ともに$\lambda$を$10^{3}, 10^{4}, 10^{5}$とした場合を評価してみました。それ以外のパラメータは、airPLS法では差分階数diffを2、arPLS法では収束判定条件ratioを0.001としました。
- airPLS法
- arPLS法
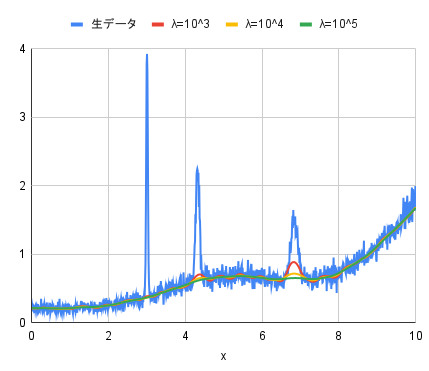
airPLS法、arPLS法ともに$\lambda$が$10^{5}$のときがもっともきれいなバックグラウンドが引けているように見えます。
両者の違いとして、バックグラウンドの高さが挙げられます。airPLS法がノイズの低いレベルにバックグラウンドが合わせられているのに対し、arPLS法はノイズの中心レベルにバックグラウンドが合わせられています。arPLS法のほうがより自然なベースラインといった感じです。
まとめ
airPLS法とarPLS法によるバックグラウンド推定を紹介しました。動作の概要をまとめると以下のようになります。
- airPLS法
- 大きな$\lambda$を与え、Whittaker Smootherを適用する。重みはすべて1とする。
- 元データと比較し、$y_{i} \geqq z_{i}$となる点の重みを0とし、そうでない点は$e^{\frac{t|y_{i} – z_{i}|}{|\mathbf{d}|}}$とする。
- 再びWhittaker Smootherを適用する。
- 再び2を実行し、$|\mathbf{d}| < 0.001 \times |\mathbf{y}|$を満たすまで繰り返す。
- arPLS法
- 大きな$\lambda$を与え、Whittaker Smootherを適用する。重みはすべて1とする。
- 元データと比較し、$y_{i} \geqq z_{i}$となる点の重みを$\frac{1}{1 +\exp\left({\frac{2(d_{i} – (-m_{\mathbf{d}^{-}}+2\sigma_{\mathbf{d}^{-}}))}{2\sigma_{\mathbf{d}^{-}}}}\right)}$とし、そうでない点は1とする。
- 再びWhittaker Smootherを適用する。
- 再び2を実行し、$\frac{|\mathbf{w}^{t} – \mathbf{w}^{t + 1}|}{|\mathbf{w}^{t}|} < ratio$を満たすまで繰り返す。

ディスカッション
コメント一覧
まだ、コメントがありません