【C++】【Eigen】最急降下法を実装する
ある関数の最小値(極小値)を探索する手法の1つである最急降下法(Gradient Descent)について調べてみたので、以下にまとめました。C++での実装例も紹介します。
1変数関数の最急降下法
原理
最急降下法は、目的関数の勾配(傾き)を用いて関数の最小値(極小値)を求める方法です。今、1次微分可能なある関数$y = f(x)$を考えます。この関数の点$(x_{k}, f(x_{k}))$における傾きは、
$$
\displaystyle
\nabla{f}_{k} = \frac{\mathrm{d}f(x_{k})}{\mathrm{d}x} \tag{1}
$$
であらわされます(下図)。
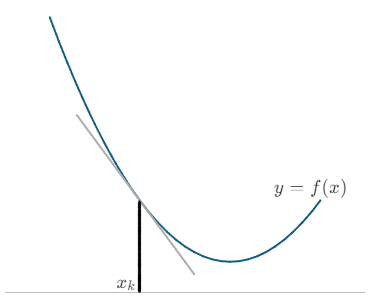
この図において、最小値方向に$x$を更新するには、$(1)$を用いると以下のようにあらわせます。
$$
\displaystyle
x_{k+1} = x_{k} – \alpha_{k}\nabla{f}_{k} \tag{2}
$$
ここで$\alpha_{k}$は$\alpha_{k} \gt 0$の適当な係数で、ステップ幅と呼ばれます。このように更新された新たな点$x_{k+1}$において、再び傾き$\nabla{f}_{k+1}$を求め、最小値方向に$x$を更新します。これを繰り返していくと、最終的には傾きが$0$の点に到達します。この点が解となります。
実際には傾きが$0$になる点に到達することはほぼないので、閾値$\epsilon$を設け、$|\nabla{f}_{k}| \lt \epsilon$となった場合や$|x_{k+1} – x_{k}| \lt \epsilon$となった場合に収束したと判定します。
ステップ幅$\alpha$の探索
式$(2)$において適当な係数$\alpha_{k}$が出てきました。この$\alpha_{k}$はハイパーパラメータで、適当な定数を与えてもよいのですが、値によっては$f(x_{k+1}) \geqq f(x_{k})$となってしまい、収束しません。そこで、適切な$\alpha_{k}$を求めるための条件があります。それがArmijo(アルミホ)の条件とWolfe(ウルフ)の条件です。
Armijoの条件
Armijoの条件は、関数値が十分に減少することを要求する条件です。具体的には$\alpha$の関数として、
$$
\displaystyle
g(\alpha) = f(x_{k} – \alpha\nabla{f}_{k})
$$
を考えます。これを横軸を$\alpha$としたグラフであらわすと、下図のようになります。
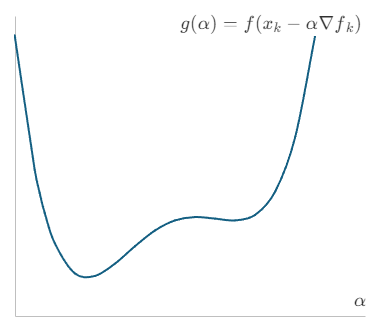
次に、点$(0, g(0))$を通る直線を$h(\alpha) = m_{0}\alpha + g(0)$を考え、傾き$m_{0}$の取りうる値を調べます。関数値が減少する必要があるので、
$$
\displaystyle
h(\alpha) \lt g(0)
$$
です。また、$g(\alpha)$の$\alpha = 0$における接線$h_{0}(\alpha)$を考えると、
$$
\displaystyle
h_{0}(\alpha) = \frac{\mathrm{d}g(0)}{\mathrm{d}\alpha}\alpha + g(0) = -(\nabla{f}_{k})^{2}\alpha + g(0)
$$
となります。この接線より傾きは大きくなければならないので、直線$h(\alpha)$の傾き$m_{0}$の取りうる値は、
$$
\displaystyle
-(\nabla{f}_{k})^{2} \lt m_{0} \lt 0
$$
となります。この時、$0 \lt c_{1} \lt 1$とすれば、$m_{0} = -c_{1} (\nabla{f}_{k})^{2}$で表すことができます。
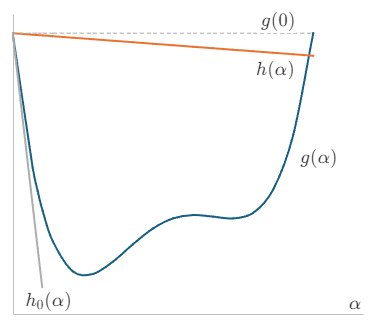
この$h(\alpha)$を基準線として、
$$
\displaystyle
g(\alpha) \leqq h(\alpha)
$$
を満たすような$\alpha$が関数値が減少するステップ数$\alpha$になります。これがArmijoの条件で、展開すると
$$
\displaystyle
f(x_{k} – \alpha\nabla{f}_{k}) \leqq f(x_{k}) – c_{1}\alpha(\nabla{f}_{k})^{2} \tag{3}
$$
で示されます。
Wolfeの条件
Wolfeの条件は、Armijoの条件にさらに曲率条件と呼ばれる制約を加えたものです。今、点$\alpha_{0}$で関数$g(\alpha)$に接する接線$l_{0}(\alpha)$を考えます。この傾きを$m_{1}$としたとき、$m_{1}$の取りうる条件を考えます。
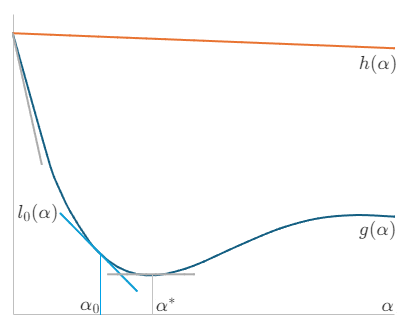
接点$\alpha_{0}$を$\alpha_{0} = 0$から大きくしていくと、やがて極小点$\alpha^{*}$に到達します。このときの接線の傾き$m_{1}$は$\frac{\mathrm{d}g(0)}{\mathrm{d}\alpha}(\lt 0)$から徐々に大きくなりながら$0$に到達します。すなわち、
$$
\displaystyle
\frac{\mathrm{d}g(0)}{\mathrm{d}\alpha} \lt m_{1} \lt 0
$$
です。今、$0 \lt c_{2} \lt 1$とすれば、$m_{1} = c_{2} \frac{\mathrm{d}g(0)}{\mathrm{d}\alpha} = -c_{2}(\nabla{f}_{k})^{2}$で表すことができます。
$l_{0}(\alpha)$の傾き$m_{1}$を傾きの基準としたとき、極小点$\alpha^{*}$を探索するためには、傾きがこれより大きい必要があります。すなわち、
$$
\displaystyle
\frac{\mathrm{d}g(\alpha)}{\mathrm{d}\alpha} = -\nabla{f}(x_{k} – \alpha\nabla{f}_{k})\nabla{f}_{k} \geqq -c_{2}(\nabla{f}_{k})^{2} \tag{4}
$$
です。次に、$c_{1}$と$c_{2}$の関係についてみていきます。$l_{0}(\alpha)$と別の接線$l(\alpha)$を考えます。接点を$\alpha_{1}(\ne \alpha_{0})$とし、$l(\alpha)$の傾きは$(4)$の条件を満たすものとします。今、$l(\alpha)$の傾きが$h(\alpha)$と同じとすると、
$$
\displaystyle
-\nabla{f}(x_{k} – \alpha_{1}\nabla{f}_{k})\nabla{f}_{k} = -c_{1}(\nabla{f}_{k})^{2} \gt -c_{2}(\nabla{f}_{k})^{2}
$$
が成立します。これより、$0 \lt c_{1} \lt c_{2} \lt 1$となります。以上をまとめると、Wolfeの条件は、
$$
\displaystyle
\begin{gather}
f(x_{k} – \alpha\nabla{f}_{k}) \leqq f(x_{k}) – c_{1}\alpha(\nabla{f}_{k})^{2} \\
-\nabla{f}(x_{k} – \alpha\nabla{f}_{k})\nabla{f}_{k} \geqq -c_{2}(\nabla{f}_{k})^{2} \\
0 \lt c_{1} \lt c_{2} \lt 1
\end{gather}
$$
となります。
C++による実装例
1変数関数の最急降下法をC++を使って実装した例を示します。例として、2次関数$f(x) = 3(x – 0.5)^{2} + 1$の最小値を最急降下法で求めてみます。この関数は解析的に最小値が求められ、$x_{\mathrm{min}} = 0.5$です。
ラムダ式で関数$f$とその微分$g$を与え、$x$の初期値を適当に与えた後に、GradientDescent()を呼び出して計算します。なお、テンプレートで作成しているので、ラムダ式である必要はなく、operator ()を実装したクラスでも動作します。
#include <cmath>
#include <iostream>
//---------------------------------------------
// 1変数関数の最急降下法の計算
//---------------------------------------------
template <typename Func, typename Grad>
bool GradientDescent(
Func & f, Grad & g, double & x, const double eps, const unsigned int max_loop
)
{
// 関数の初期値
double old_f = f(x);
// ループ回数
unsigned int loop = 0;
// ステップ幅の初期値
double alpha = 1;
// パラメータc1, c2
const double c1 = 1e-4, c2 = 0.9;
while(true) {
// 探索方向を決める
double nabla_f = g(x);
// 直線探索の実施。ステップ幅alphaを決める
while(true){
double tmp_f = f(x - alpha * nabla_f);
double tmp_g = g(x - alpha * nabla_f);
// Wolfeの条件を用いて、alphaを探索する
if(tmp_f > old_f - c1 * alpha * nabla_f * nabla_f){
// 1番目のWolfeの条件を満たさない時はalphaが大きすぎる → 小さくする
alpha /= 2;
}
else if(-tmp_g * nabla_f >= -c2 * nabla_f * nabla_f){
// 2番目のWolfeの条件を満たすときはalphaが適正 → ループを抜ける
break;
}
else{
// 満たさない時はalphaが小さすぎる → 大きくする
alpha *= 2;
}
}
// xの更新
x = x - alpha * nabla_f;
// 更新したxの値を用いて、f(x)を計算
double new_f = f(x);
// 収束判定
if(std::fabs(new_f - old_f) < eps){
break;
}
if(loop >= max_loop){
return false;
}
loop++;
old_f = new_f;
}
std::cerr << "loop = " << loop << std::endl;
return true;
}
//---------------------------------------------
// main()関数
//---------------------------------------------
int main()
{
// xの初期値
double x0 = 0;
// 関数f
auto f = [](double x){
return 3 * (x - 0.5) * (x - 0.5) + 1;
};
// 微分g
auto g = [](double x){
return 6 * x - 3;
};
if(GradientDescent(f, g, x0, 1e-10, 100)){
std::cout << x0 << std::endl;
}
else{
std::cout << "failure." << std::endl;
}
return 0;
}出力結果
loop = 17
0.499998解析的に求めた解とほぼ同じ値が得られました。
多変数関数の最急降下法
多変数関数の最急降下法も1変数関数の最急降下法と考え方は同じです。関数$y = f(\boldsymbol{x})$について考えます。$\boldsymbol{x} = (x_{0}, \dots, x_{n})$とします。点$\boldsymbol{x}_{k}$における勾配ベクトルを
$$
\displaystyle
\nabla{\boldsymbol{f}_{k}} = \begin{pmatrix}
\frac{\partial{f(\boldsymbol{x}_{k})}}{\partial{x_{0}}} \\
\vdots \\
\frac{\partial{f(\boldsymbol{x}_{k})}}{\partial{x_{n}}}
\end{pmatrix}
$$
と置くと、最小値方向に$\boldsymbol{x}$を更新するには、以下のようにあらわせます。
$$
\displaystyle
\boldsymbol{x}_{k+1} = \boldsymbol{x}_{k} – \alpha_{k}\nabla{\boldsymbol{f}}_{k}
$$
Armijoの条件やWolfeの条件も考え方は同じで、$\nabla{\boldsymbol{f}_{k}}$がベクトルであることに注意すれば、以下のようになります。
- Armijoの条件
$$
\displaystyle
\begin{gather}
f(\boldsymbol{x}_{k} – \alpha\nabla{\boldsymbol{f}}_{k}) \leqq f(\boldsymbol{x}_{k}) – c_{1}\alpha(\nabla{\boldsymbol{f}}_{k})^{T}\nabla{\boldsymbol{f}_{k}} \\
0 \lt c_{1} \lt 1
\end{gather}
$$
- Wolfeの条件
$$
\begin{gather}
\displaystyle
f(\boldsymbol{x}_{k} – \alpha\nabla{\boldsymbol{f}}_{k}) \leqq f(\boldsymbol{x}_{k}) – c_{1}\alpha(\nabla{\boldsymbol{f}}_{k})^{T}\nabla{\boldsymbol{f}_{k}} \\
-\nabla{\boldsymbol{f}}(\boldsymbol{x}_{k} – \alpha\nabla{\boldsymbol{f}}_{k})^{T}\nabla{\boldsymbol{f}}_{k} \geqq -c_{2}(\nabla{\boldsymbol{f}}_{k})^{T}\nabla{\boldsymbol{f}_{k}} \\
0 \lt c_{1} \lt c_{2} \lt 1
\end{gather}
$$
Eigenによる実装例
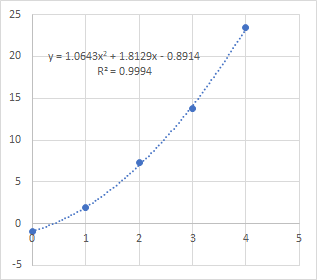
多変数関数の最急降下法をC++とEigenを使って実装した例を示します。例として、点$(x, y) = (0, -0.9), (1, 1.9), (2, 7.3), (3, 13.8), (4, 23.5)$に対し、2次関数$f(x) = a_{0} + a_{1} x + a_{2} x^{2}$で最小二乗法
$$
\displaystyle
S =\frac{1}{2}\sum_{i=1}^{5}(y_{i} – f(x_{i}))^{2} \tag{n}
$$
を用いて回帰してみました。この場合、最小値を求めるのは、$f(x)$ではなく$S$です。なので$S$に対して最急降下法を適用します。また、求めたいものは$\boldsymbol{a} = (a_{0}, a_{1}, a_{2})$です。したがって、$S$を$a_{j}$で偏微分したものを勾配として扱います。
$$
\displaystyle
\nabla\boldsymbol{S}_{k} = \begin{pmatrix}
\frac{\partial{S}}{\partial{a_{0}}^{(k)}} \\
\frac{\partial{S}}{\partial{a_{1}}^{(k)}} \\
\frac{\partial{S}}{\partial{a_{2}}^{(k)}}
\end{pmatrix}
= -\begin{pmatrix}
\sum_{i=1}^{5}\frac{\partial{f(x_{i})}}{\partial{a_{0}^{(k)}}}(y_{i} – f(x_{i})) \\
\sum_{i=1}^{5}\frac{\partial{f(x_{i})}}{\partial{a_{1}^{(k)}}}(y_{i} – f(x_{i})) \\
\sum_{i=1}^{5}\frac{\partial{f(x_{i})}}{\partial{a_{2}^{(k)}}}(y_{i} – f(x_{i}))
\end{pmatrix}
$$
と置くと、$\boldsymbol{a}$は
$$
\displaystyle
\boldsymbol{a}^{(k+1)}=\boldsymbol{a}^{(k)} – \alpha_{k}\nabla\boldsymbol{S}_{k}
$$
で更新されます。実際のコードは以下になります。
#include <iostream>
#include <Eigen/Eigen>
//---------------------------------------------
// 多変数関数の最急降下法の計算
//---------------------------------------------
template <typename Func, typename Grad>
bool GradientDescent(
Func & f, Grad & g, Eigen::VectorXd & a, Eigen::VectorXd & x, Eigen::VectorXd & y,
const double eps, const unsigned int max_loop)
{
// 関数fの初期値
double old_f = f(a, x, y);
// ループ回数
unsigned int loop = 0;
// ステップ幅の初期値
double alpha = 1;
// パラメータc1, c2
const double c1 = 1e-4, c2 = 0.9;
while(true){
// 探索方向を決める
Eigen::VectorXd nabla_f = g(a, x, y);
double p = nabla_f.transpose() * nabla_f;
// 直線探索の実施。ステップ幅alphaを決める
while(true){
Eigen::VectorXd a_tmp = a - alpha * nabla_f;
double tmp_f = f(a_tmp, x, y);
Eigen::VectorXd tmp_nabla_f = g(a_tmp, x, y);
// Wolfeの条件を用いて、alphaを探索する
if(tmp_f > old_f - c1 * alpha * p){
// 1番目のWolfeの条件を満たさない時はalphaが大きすぎる → 小さくする
alpha /= 2;
}
else if(-tmp_nabla_f.transpose() * nabla_f >= -c2 * p){
// 2番目のWolfeの条件を満たすときはalphaが適正 → ループを抜ける
break;
}
else{
// 満たさない時はalphaが小さすぎる → 大きくする
alpha *= 2;
}
}
a = a - alpha * nabla_f;
// 更新したaの値を用いて、f(a, x, y)を計算
double new_f = f(a, x, y);
// 収束判定
if(std::fabs(new_f - old_f) < eps){
break;
}
if(loop >= max_loop){
return false;
}
loop++;
old_f = new_f;
}
std::cerr << "loop = " << loop << std::endl;
return true;
}
//---------------------------------------------
// main()関数
//---------------------------------------------
int main()
{
Eigen::VectorXd param_a(3), data_x(5), data_y(5);
param_a << 1, 1, 1;
data_x << 0, 1, 2, 3, 4;
data_y << -0.9, 1.9, 7.3, 13.8, 23.5;
// 関数f
auto f = [](Eigen::VectorXd & a, double x){
return a(0) + a(1) * x + a(2) * x * x;
};
// 勾配ベクトルg
auto g = [](Eigen::VectorXd & a, double x){
Eigen::VectorXd ret(3);
ret << 1, x, (x * x);
return ret;
};
// 関数S
auto s = [&f](Eigen::VectorXd & a, Eigen::VectorXd & x, Eigen::VectorXd & y){
double sum = 0;
for(int i = 0; i < x.size(); i++){
double t = y(i) - f(a, x(i));
sum += t * t;
}
return sum / 2;
};
// Sの勾配ベクトル
auto nabla_s = [&f, &g](Eigen::VectorXd & a, Eigen::VectorXd & x, Eigen::VectorXd & y){
Eigen::VectorXd sum = Eigen::VectorXd::Zero(a.size());
for(int i = 0; i < x.size(); i++){
double t = y(i) - f(a, x(i));
sum += -g(a, x(i)) * t;
}
return sum;
};
if(GradientDescent(s, nabla_s, param_a, data_x, data_y, 1.0e-10, 10000)){
std::cout << param_a << std::endl;
}
else{
std::cout << "failure." << std::endl;
}
return 0;
}ラムダ式で関数$f$とその偏微分$g$を与え、係数$a$の初期値を適当に与えた後に、GradientDescent()を呼び出して計算します。なお、テンプレートで作成しているので、ラムダ式である必要はなく、operator ()を実装したクラスでも動作します。
出力結果
loop = 2011
-0.889754
1.81072
1.06474Excelで散布図を作り、2次関数で回帰した結果と比較しました。ほぼ同様の値が得られていることがわかります。なお、最急降下法の収束はかなり緩やかで、精度よく求めようとすると多数の反復が必要です。
まとめ
最急降下法について説明とC++による実装例を紹介しました。
アルゴリズムについてまとめると以下のようになります。
最急降下法のアルゴリズム
- パラメータ$\boldsymbol{x}$の初期値を決める
- 関数$f$を計算する
- 関数$f$の勾配ベクトル$\nabla{\boldsymbol{f}}_{k}$を計算する
- パラメータ$\alpha$と勾配ベクトル$\nabla{\boldsymbol{f}}_{k}$を用いて$\boldsymbol{x}$を更新する
- 関数$f$を計算する
- 関数$f$の変化量がしきい値以下なら計算終了
- 3に戻る


ディスカッション
コメント一覧
まだ、コメントがありません